Properties of Networks Homework

Figure 1. Risk Board Accessibility Network

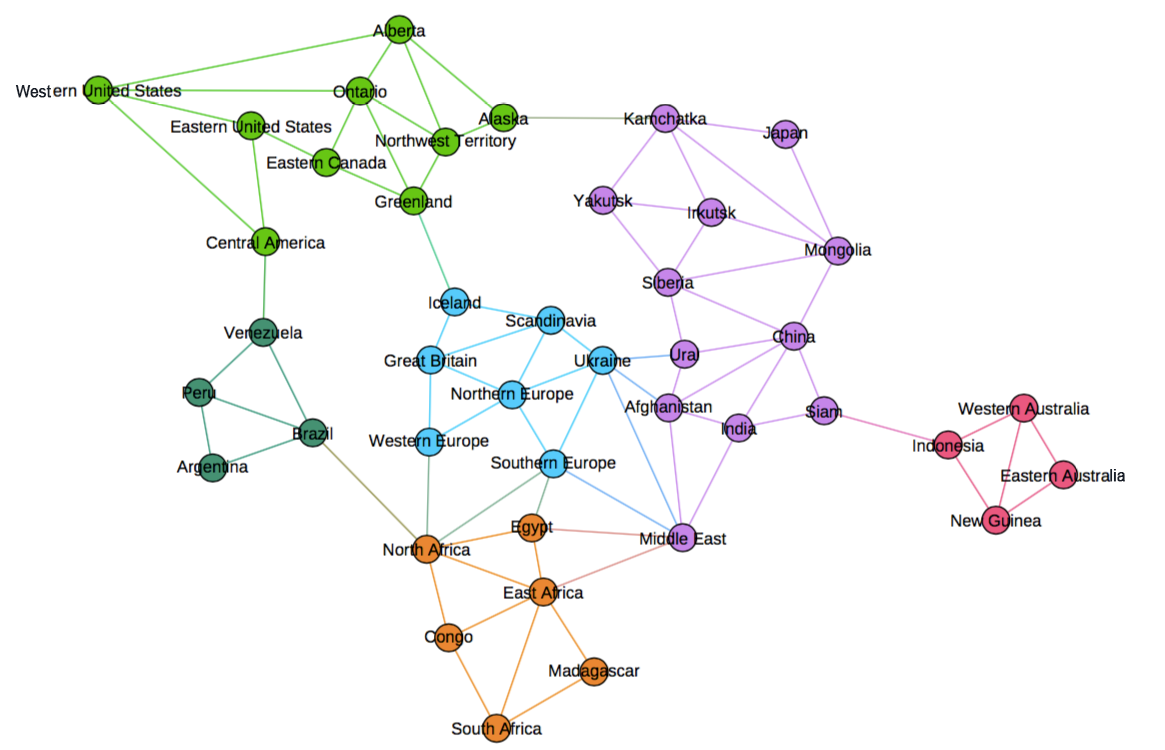
For the following questions, refer to Figure 1.

Node Properties

1. Identify which node(s) have the highest degree and state this degree.

   • ANSWER: For the Risk board, Ukraine, East Africa, North Africa, China, and the Middle East all have a degree of 6. For the Metro map, node N has a degree of 5.

2. Identify which node(s) have the highest degree centrality and this metric's value.

   • ANSWER: For the Risk board, Ukraine, East Africa, North Africa, China, and the Middle East are all tied for highest degree centrality, with a normalized score of 0.1463. In the Metro map, node N has the highest degree centrality at 0.2778.

3. Identify which node(s) have the highest closeness centrality and this metric's value.

   • ANSWER: In Risk, Ukraine has the highest closeness centrality at 0.3203. For the Metro map, it's still node N at 0.45.

4. Identify which node(s) have the highest betweenness centrality and this metric's value.

   • ANSWER: North Africa has the highest betweenness centrality for Africa, with 0.2133. Node N still has the highest betweenness for the Metro map at 0.5163.

5. Compare the node sets for each of these centrality measures. Are they the same? If not, provide a brief discussion on why you think they are different.

   • ANSWER FOR RISK BOARD: For the Risk board, we see some differences among the three centrality measures: The set of nodes with highest degree centrality contains the nodes with highest closeness and betweenness centrality, but Ukraine is the average closest node, whereas North Africa is the best bridging node with highest betweenness centrality. I posit they are different because, while Ukraine has the most access to different countries, North Africa provides a gateway to all of Africa and South America.

   • ANSWER FOR METRO MAP: Node N is consistently the most central node across all three metrics.

Graph Properties

1. Calculate the connectivity/cohesion for this graph.

   • ANSWER: The connectivity for the Risk board is 1. If we delete the link between Siam and Indonesia, we have disconnected the graph and left Australia alone.

2. Draw the 1-degree egocentric network for node Ukraine.

   • ANSWER:

     

3. Draw the 1.5-degree egocentric network for node Ukraine and calculate this network's density.

   • ANSWER: With Ukraine, the density is 0.5238

     

   • ANSWER: If you remove Ukraine from the 1.5-degree ego-net, the density is 0.3333.

     

4. Calculate the local clustering coefficient for nodes Ukraine, Congo, and Argentina.

   • ANSWER: Ukraine's LCC is 0.3333, Congo's is 0.6667, and Argentina's is 1.0.

Figure 2. DC Metro Map

For the remaining questions, refer to Figure 2.

1. Using the same number of nodes, draw a graph with the highest unnormalized degree centralization score.

   • ANSWER: The star graph is generally a good example of a highly centralized network, and most graphs with the maximum centralization have this form.

     

2. Calculate the degree centralization score of the graph you are given; then calculate its normalized degree centralization value using your graph above.

   • ANSWER: The degree centralization score for the metro graph is 3.056.

     

     

   • To normalize this centralization score, we need to divide by the maximum possible centralization metric for a network with the same number of nodes (i.e., the graph you constructed above), which results in a normalized centralization of 3.056 / 17 = 0.1797.